感谢快速傅里叶变换(FFT)超详解 - 知乎 (zhihu.com)为本蒟蒻带来的解惑
前置芝士
点值表示:对于一个 $n$ 次多项式 $f(x)$ ,可以通过 $n+1$ 个不同的 $x$ 带入函数解得系数
表示为 $((x_1,f(x_1)),(x_2,f(x_2)),(x_3,f(x_3))…(x_n,f(x_n)))$
称这种表示方法为点值表示
单位根:在复平面上,以单位圆点( $1$ )为起点,单位圆的 $n$ 等分点(还是1)为终点,在单位圆上可以得到n个复数,设幅角为正且最小的复数为 $\omega_n$ ,称为 $n$ 次单位根。
复平面:众所周知复数可以表示为 $a+bi,(i=\sqrt{-1},a\in R,b\in R)$ 那么用 $x$ 轴坐标表示 $a$, $y$ 轴坐标表示 $b$ ,即为复平面。
欧拉公式: $e^{ix}=\cos x+i\sin x$
如图为 $17$ 边时:
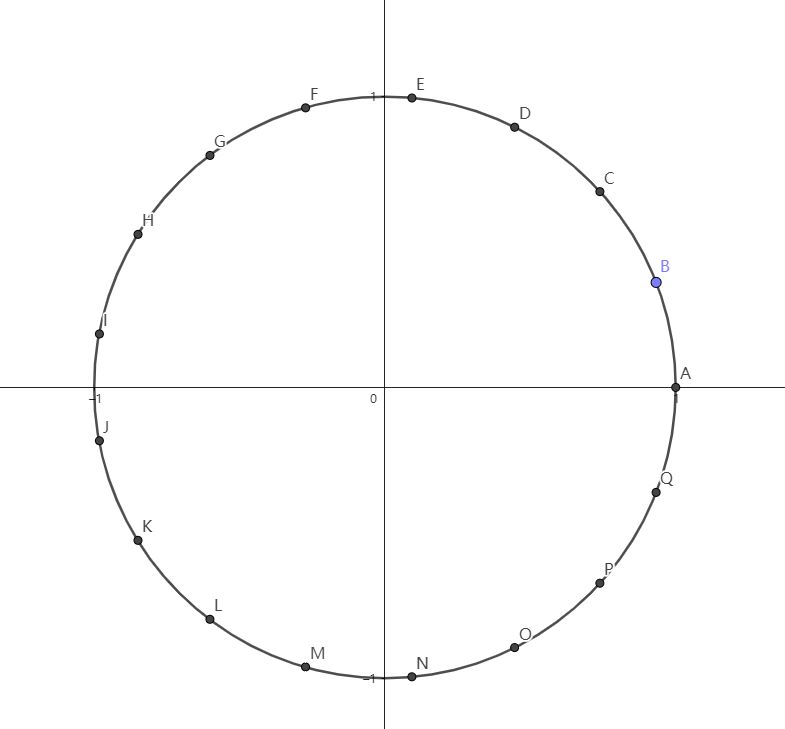
那么$\omega_n=\cos \frac{2\pi}{n}+i\ \sin\frac{2\pi}{n}$
令 $x=\frac{2\pi}{n} $
则有 $e^{ix}=\omega_n$
故 $\omega_n^k=e^{ikx}=\cos \frac{2k\pi}{n}+i\sin \frac{2k\pi}{n}=k\omega_n$
$\omega_n^k=\omega_{2n}^{2k}$
$\omega_n^{k+\frac{n}{2}}=\omega_n^k\cdot\left(\cos \pi+i\sin\pi\right)=-\omega_n^k$
易证 $\omega_n^{k}\cdot\omega_n^{n-k}=1$
正式开始
普通FFT
对于一个有 $n$ 项的多项式 $f(x)=\sum_{i=0}^{n-1}a_ix^i$
我们把 $n$ 变为第一个 $\ge n$ 的 $2^s$ ,没有的项 $a_i=0$
即
$f(x)=a_0+a_1x^1+a_2x^2+a_3x^3…+a_{n-1}x^{n-1}$
按奇偶分类
$f_1(x)=a_0+a_2x+a_4x^2…+a_{n-2}x^{\frac{n-2}{2}}$
$f_2(x)=a_1+a_3x+a_5x^2…+a_{n-1}x^{\frac{n}{2}}$
$f(x)=f_1(x^2)+xf_2(x^2)$
令 $x=\omega_n^k$
即 $f(\omega_n^k)=f_1(\omega_{n}^{2k})+\omega_{n}^{k}f_2(\omega_n^{2k})=f_1(\omega_{\frac{n}{2}}^k)+\omega_{n}^{k}f_2(\omega_{\frac{n}{2}}^k)$
同理, $f(\omega_n^{k+\frac{n}{2}})=f_1(\omega_{\frac{n}{2}}^{k})-\omega_n^kf_2(\omega_\frac{n}{2}^k)$ (这个很重要,因为同时求了两个数复杂度才是 $O(\log_2n)$,不然就是 $ O(n)$
以及
$$
\begin{aligned}
f(\omega_n^{n-k})&=\cos \frac{2(n-k)\pi}{n}+i\sin\frac{2(n-k)\pi}{n}\\
&=\cos(2\pi-\frac{2k\pi}{n})+i\sin(2\pi-\frac{2k\pi}{n})\\
&=\cos\frac{2k\pi}{n}-i\sin\frac{2k\pi}{n}
\end{aligned}
$$
递归到 $n=1$ 即可,此时函数值为 $1$
此时我们成功在 $n\log n$ 复杂度求出了点值表示
接下来要转化为系数表示
$$
\begin{aligned}
&f(\omega_n^1)=\sum_{i=0}^na_i(\omega_n^1)^i=x_1(x_1为已经求出来的数)\\
&f(\omega_n^2)=\sum_{i=0}^na_i(\omega_n^2)^i=x_2\\
&\vdots\\
\end{aligned}
$$
那么写成矩阵:
$$
\left[
\begin{array}{}
(\omega_n^0)^0 & (\omega_n^0)^1 & (\omega_n^0)^2 & (\omega_n^0)^3&\cdots&(\omega_n^0)^n\\
(\omega_n^1)^0 & (\omega_n^1)^1 & (\omega_n^1)^2 & (\omega_n^1)^3&\cdots&(\omega_n^1)^n\\(\omega_n^2)^0 & (\omega_n^2)^1 & (\omega_n^2)^2 & (\omega_n^2)^3&\cdots&(\omega_n^2)^n\\
(\omega_n^3)^0 & (\omega_n^3)^1 & (\omega_n^3)^2 & (\omega_n^3)^3&\cdots&(\omega_n^3)^n\\
\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{n-1})^0 & (\omega_n^{n-1})^1 & (\omega_n^{n-1})^2 & (\omega_n^{n-1})^3&\cdots&(\omega_n^{n-1})^n\\
\end{array}
\right]
\left[
\begin{array}{}
a_0\\a_1\\a_2\\a_3\\\vdots\\a_{n-1}\\
\end{array}
\right]=
\left[
\begin{array}{}
x_0\\x_1\\x_2\\x_3\\\vdots\\x_{n-1}\\
\end{array}
\right]
$$
找到上面左边这个矩阵的逆矩阵 $A$ 就可以将 $A$ 和点值表示 $x$ 相乘,同先前部分处理。
那么问题转化为求它的逆矩阵
有一个东西
$$
x^n=1\\
x^n-1=(x-1)(x^{n-1}+x^{n-2}+x^{n-3}\cdots+1)\\
$$
若 $x=1$
则 $x^{n-1}+x^{n-2}+\cdots+1=n$
否则 $x-1\neq 0$ 即 $x^{n-1}+x^{n-2}+\cdots+1=0$
$$
\left[
\begin{array}{}
(\omega_n^i)^0&(\omega_n^i)^1&(\omega_n^i)^2\cdots(\omega_n^i)^{n-1}
\end{array}
\right]
\left[
\begin{array}{}
(\omega_n^{n-j})^0\\(\omega_n^{n-j})^1\\(\omega_n^{n-j})^2\\\vdots\\(\omega_n^{n-j})^{n-1}\\
\end{array}
\right]
=\sum_{k=0}^{n-1}(\omega_n^{n+i-j})^k
$$
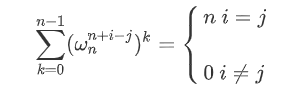
是不是很眼熟?
$$
\left[
\begin{array}{}
(\omega_n^0)^0&(\omega_n^0)^1&(\omega_n^0)^2&\cdots&(\omega_n^0)^{n-1}\\
(\omega_n^1)^0&(\omega_n^1)^1&(\omega_n^1)^2&\cdots&(\omega_n^1)^{n-1}\\
(\omega_n^2)^0&(\omega_n^2)^1&(\omega_n^2)^2&\cdots&(\omega_n^2)^{n-1}\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&(\omega_n^{n-1})^2&\cdots&(\omega_n^{n-1})^{n-1}\\
\end{array}
\right]
\left[
\begin{array}{}
(\omega_n^{n})^0&(\omega_n^{n-1})^0&(\omega_n^{n-2})^0&\cdots&(\omega_n^{1})^{0}\\
(\omega_n^{n})^1&(\omega_n^{n-1})^1&(\omega_n^{n-2})^1&\cdots&(\omega_n^{1})^{1}\\
(\omega_n^{n})^2&(\omega_n^{n-1})^2&(\omega_n^{n-2})^2&\cdots&(\omega_n^{1})^{2}\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{n})^{n-1}&(\omega_n^{n-1})^{n-1}&(\omega_n^{n-2})^{n-1}&\cdots&(\omega_n^{1})^{n-1}\\
\end{array}
\right]=
\left[
\begin{array}{}
n&0&0&0&\cdots&0\\
0&n&0&0&\cdots&0\\
0&0&n&0&\cdots&0\\
0&0&0&n&\cdots&0\\
\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\
0&0&0&0&\cdots&n
\end{array}
\right]\\
$$
整体乘上 $\frac{1}{n}$ 就是单位矩阵
逆矩阵即为
$$
\left[
\begin{array}{}
(\omega_n^{n})^0&(\omega_n^{n})^1&(\omega_n^{n})^2&\cdots&(\omega_n^{n})^{n-1}\\
(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&(\omega_n^{n-1})^2&\cdots&(\omega_n^{n-1})^{n-1}\\
(\omega_n^{n-2})^0&(\omega_n^{n-2})^1&(\omega_n^{n-2})^2&\cdots&(\omega_n^{n-2})^{n-1}\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
(\omega_n^{1})^0&(\omega_n^{1})^1&(\omega_n^{1})^2&\cdots&(\omega_n^{1})^{n-1}\\
\end{array}
\right]
$$
又 $\omega_n^{n-k}=\cos\frac{2k\pi}{n}-i\sin\frac{2k\pi}{n}$
则在后面累计时用一个 $inv$ 记录符号即可
view code
1 | void getF(complex<double>*a,int n,int inv){ |
优化
三次变两次
原理:
$$
(a+bi)^2=a^2-b^2+2abi
$$
那么将 $g(x)$ 存在 $f(x)$ 的虚部上, $ans$ 即为虚部上的数 $\div2$
蝶形变换
递归的形式往往都可以变成递推
观察每次分组时是二进制下 $i$ 位为 $1$ 就是分到前面,$0$ 就分到后面
如图
观察得 $\omega_n^i$ 在原数组中的位置为 $i$ 二进制翻转得到的数